Subsets
Question
Problem Statement
Given a set of distinct integers, nums, return all possible subsets.
Note: The solution set must not contain duplicate subsets.
For example,
If nums = [1,2,3], a solution is:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
题解
子集类问题类似Combination,以输入数组[1, 2, 3]分析,根据题意,最终返回结果中子集类的元素应该按照升序排列,故首先需要对原数组进行排序。题目的第二点要求是子集不能重复,至此原题即转化为数学中的组合问题。我们首先尝试使用 DFS 进行求解,大致步骤如下:
[1] -> [1, 2] -> [1, 2, 3][2] -> [2, 3][3]
将上述过程转化为代码即为对数组遍历,每一轮都保存之前的结果并将其依次加入到最终返回结果中。
Iterative
Python
class Solution:
"""
@param S: The set of numbers.
@return: A list of lists. See example.
"""
def subsets(self, S):
if not S:
return []
ret = []
S.sort()
n = len(S)
# 000 -> []
# 001 -> [1]
# 010 -> [2]
# ...
# 111 -> [1, 2, 3]
for i in xrange(2**n):
tmp = []
for j in xrange(n):
if i & (1 << j):
tmp.append(S[j])
ret.append(tmp)
return ret
源码分析
利用类似bit map的原理, 将 0 ~ 个数值map到每个index上,如果index数值为1,就将该number加入。比如输入是[1 ,2 ,3], 那么当i = 0时,0也就是000, 那么000 -> []; 当i = 1时, 001 -> [1]; 直到i = 7, 111 -> [1, 2, 3].
Recursive
Python
class Solution:
# @param {integer[]} nums
# @return {integer[][]}
def subsets(self, nums):
if nums is None:
return []
result = []
nums.sort()
self.dfs(nums, 0, [], result)
return result
def dfs(self, nums, pos, list_temp, ret):
# append new object with []
ret.append([] + list_temp)
for i in xrange(pos, len(nums)):
list_temp.append(nums[i])
self.dfs(nums, i + 1, list_temp, ret)
list_temp.pop()
less code style
class Solution:
"""
@param S: The set of numbers.
@return: A list of lists. See example.
"""
def subsets(self, S):
ret = []
self.helper(sorted(S), ret, [])
return ret
def helper(self, vals, ret, tmp):
ret.append(tmp[:])
for i, val in enumerate(vals):
self.helper(vals[i + 1:], ret, tmp + [val])
C++
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int> > result;
if (nums.empty()) return result;
sort(nums.begin(), nums.end());
vector<int> list;
dfs(nums, 0, list, result);
return result;
}
private:
void dfs(vector<int>& nums, int pos, vector<int> &list,
vector<vector<int> > &ret) {
ret.push_back(list);
for (int i = pos; i < nums.size(); ++i) {
list.push_back(nums[i]);
dfs(nums, i + 1, list, ret);
list.pop_back();
}
}
};
Java
public class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> result = new ArrayList<List<Integer>>();
List<Integer> list = new ArrayList<Integer>();
if (nums == null || nums.length == 0) {
return result;
}
Arrays.sort(nums);
dfs(nums, 0, list, result);
return result;
}
private void dfs(int[] nums, int pos, List<Integer> list,
List<List<Integer>> ret) {
// add temp result first
ret.add(new ArrayList<Integer>(list));
for (int i = pos; i < nums.length; i++) {
list.add(nums[i]);
dfs(nums, i + 1, list, ret);
list.remove(list.size() - 1);
}
}
}
源码分析
Java 和 Python 的代码中在将临时list 添加到最终结果时新生成了对象,(Python 使用[] +), 否则最终返回结果将随着list 的变化而变化。
Notice: backTrack(num, i + 1, list, ret);中的『i + 1』不可误写为『pos + 1』,因为pos用于每次大的循环,i用于内循环,第一次写subsets的时候在这坑了很久... :(
回溯法可用图示和函数运行的堆栈图来理解,强烈建议使用图形和递归的思想分析,以数组[1, 2, 3]进行分析。下图所示为list及result动态变化的过程,箭头向下表示list.add及result.add操作,箭头向上表示list.remove操作。
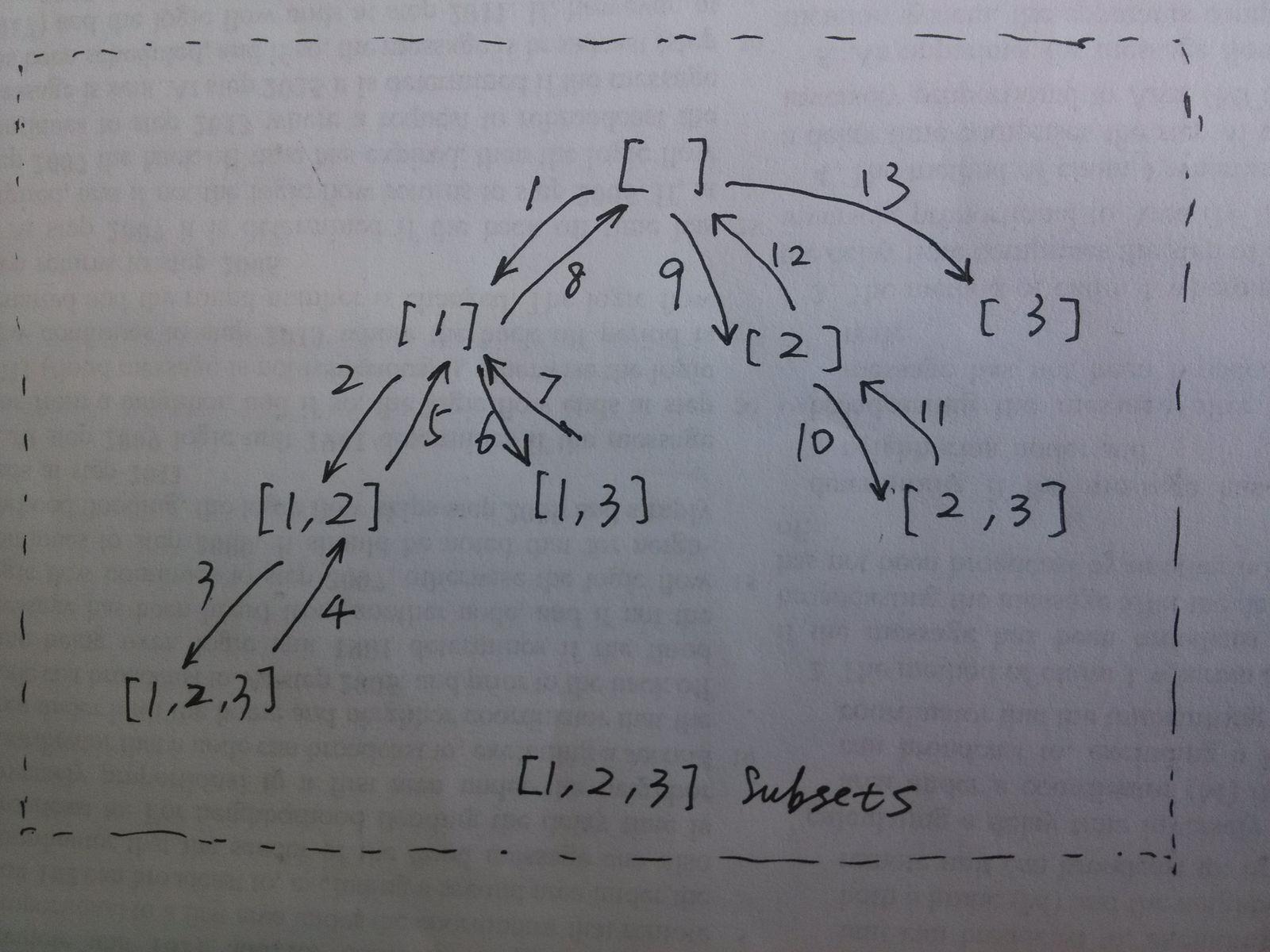
复杂度分析
对原有数组排序,时间复杂度近似为 . 状态数为所有可能的组合数 , 生成每个状态所需的时间复杂度近似为 , 如[1] -> [1, 2], 故总的时间复杂度近似为 .
使用了临时空间list保存中间结果,list 最大长度为数组长度,故空间复杂度近似为 .
