Search in Rotated Sorted Array

Question

• leetcode: (33) Search in Rotated Sorted Array
• lintcode: (62) Search in Rotated Sorted Array

Problem Statement

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Example

For [4, 5, 1, 2, 3] and target=1, return 2.

For [4, 5, 1, 2, 3] and target=0, return -1.

Challenge

O(logN) time

Solution1 - work on sorted subarray

Draw it. Rotated sorted array will take one of the following two forms:

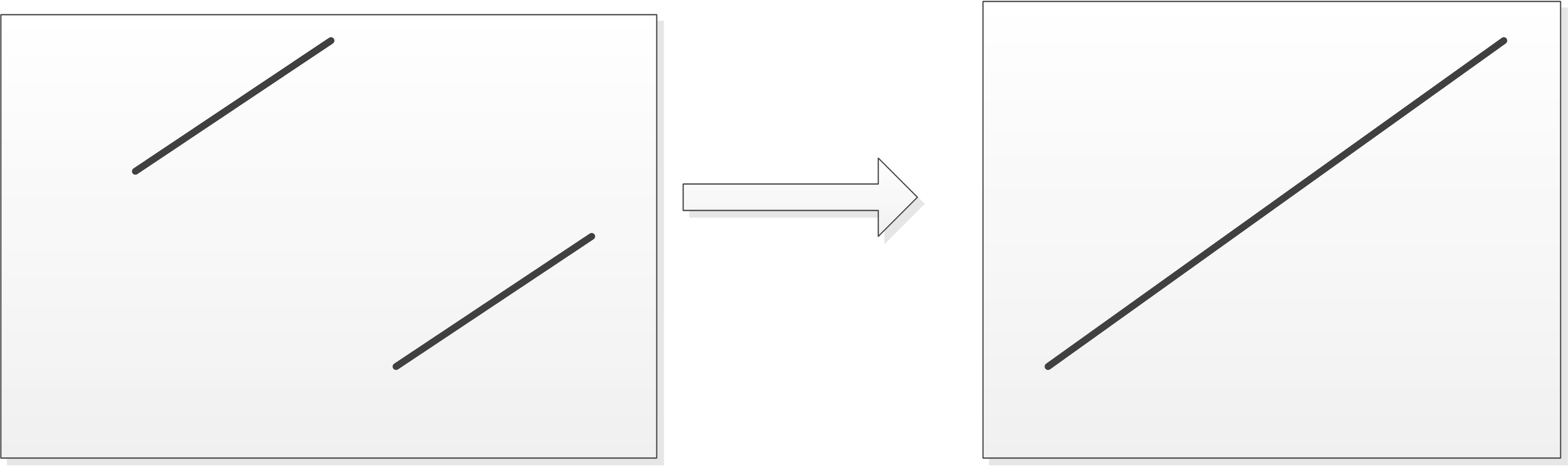
Binary search does well in sorted array, while this problem gives an unordered one. Be patient. It is actually a combination of two sorted subarrayss. The solution takes full advantage of this. BTW, another approach can be comparing target with A[mid], but dealing with lots of cases is kind of sophisticated.

C++

/**
 * 本代码fork自
 * http://www.jiuzhang.com/solutions/search-in-rotated-sorted-array/
 */
class Solution {
    /**
     * param A : an integer ratated sorted array
     * param target :  an integer to be searched
     * return : an integer
     */
public:
    int search(vector<int> &A, int target) {
        if (A.empty()) {
            return -1;
        }

        vector<int>::size_type start = 0;
        vector<int>::size_type end = A.size() - 1;
        vector<int>::size_type mid;

        while (start + 1 < end) {
            mid = start + (end - start) / 2;
            if (target == A[mid]) {
                return mid;
            }
            if (A[start] < A[mid]) {
                // situation 1, numbers between start and mid are sorted
                if (A[start] <= target && target < A[mid]) {
                    end = mid;
                } else {
                    start = mid;
                }
            } else {
                // situation 2, numbers between mid and end are sorted
                if (A[mid] < target && target <= A[end]) {
                    start = mid;
                } else {
                    end = mid;
                }
            }
        }

        if (A[start] == target) {
            return start;
        }
        if (A[end] == target) {
            return end;
        }
        return -1;
    }
};

Java

public class Solution {
    /**
     *@param A : an integer rotated sorted array
     *@param target :  an integer to be searched
     *return : an integer
     */
    public int search(int[] A, int target) {
        if (A == null || A.length == 0) return -1;

        int lb = 0, ub = A.length - 1;
        while (lb + 1 < ub) {
            int mid = lb + (ub - lb) / 2;
            if (A[mid] == target) return mid;

            if (A[mid] > A[lb]) {
                // case1: numbers between lb and mid are sorted
                if (A[lb] <= target && target <= A[mid]) {
                    ub = mid;
                } else {
                    lb = mid;
                }
            } else {
                // case2: numbers between mid and ub are sorted
                if (A[mid] <= target && target <= A[ub]) {
                    lb = mid;
                } else {
                    ub = mid;
                }
            }
        }

        if (A[lb] == target) {
            return lb;
        } else if (A[ub] == target) {
            return ub;
        }
        return -1;
    }
}

Source Code Analysis

1. If target == A[mid], just return.
2. Observe the two sorted subarrays, we can find that the least one of the left is greater than the biggest of the right. So if A[start] < A[mid], then interval [start, mid] will be sorted.
3. Do binary search on A[start] ~ A[mid] on condition that A[start] <= target <= A[mid].
4. Or do binary search on A[mid]~A[end] on condition that A[mid] <= target <= A[end].
5. If while loop ends and none A[mid] hits, then examine A[start] and A[end].
6. Return -1 if target is not found.

Complexity

The time complexity is approximately O(log n).

Solution2 - double binary search

Do binary search twice: first on the given array to find the break point; then on the proper piece of subarray to search for the target.

It may take a small step to see why the given array is binary-searchable. Though a rotated array itself is neither sorted nor monotone, there is implicit monotonicity. All elements on the left of break point are ≥A[0], and those on the right of break point are <A[0]. In a binary search, we keep narrowing the search scope by dropping the left or right half of the sequence, and here in the rotated array, we can do that much similarly.

To formalize, define an array A' that A'[i] = A[i] < A[0] ? true : false . If A is [4, 5, 6, 7, 0, 1, 2], A' will be [false, false, false, false, true, true, true]. Surely A' monotone.

Java

public class Solution {
    /**
     *@param A : an integer rotated sorted array
     *@param target :  an integer to be searched
     *return : an integer
     */
    public int search(int[] A, int target) {
        if (A == null || A.length == 0) {
            return -1;
        }

        int p = findBreakPoint(A);
        if (target >= A[0]) {
            // search in [lo, segPoint]
            return binSearch(A, target, 0, p);
        } else {
            // search in [segPoint, hi]
            return binSearch(A, target, p, A.length - 1);
        }
    }

    private int findBreakPoint(int[] A) {
        // A[index] < A[0], min[index]
        int index;

        int lo = 0, hi = A.length - 1, segValue = A[0];
        while (lo + 1 < hi) {
            int md = lo + (hi - lo)/2;
            if (A[md] > segValue) {
                lo = md;
            } else {
                hi = md;
            }
        }
        index = A[lo] < segValue ? lo : hi;

        return index;
    }

    private int binSearch(int[] A, int target, int lo, int hi) {
        while (lo + 1 < hi) {
            int md = lo + (hi - lo) / 2;
            if (A[md] == target) {
                lo = md;
            } else if (A[md] < target) {
                lo = md;
            } else {
                hi = md;
            }
        }

        if (A[lo] == target) {
            return lo;
        }
        if (A[hi] == target) {
            return hi;
        }
        return -1;
    }
}

Complexity

The first binary search costs O(log n) time complexity, and the second costs no more than O(log n).