Quick Sort

out-in-place implementation
- Complexity
in-place implementation
Reference

In essence, quick sort is an application of divide and conquer strategy. There are usually three steps:

Pick a pivot -- a random element.
Partition -- put the elements smaller than pivot to its left and greater ones to its right.
Recurse -- apply above steps until the whole sequence is sorted.

out-in-place implementation

Recursive implementation is easy to understand and code. Python list comprehension looks even nicer:

#!/usr/bin/env python


def qsort1(alist):
    print(alist)
    if len(alist) <= 1:
        return alist
    else:
        pivot = alist[0]
        return qsort1([x for x in alist[1:] if x < pivot]) + \
               [pivot] + \
               qsort1([x for x in alist[1:] if x >= pivot])

unsortedArray = [6, 5, 3, 1, 8, 7, 2, 4]
print(qsort1(unsortedArray))

The output：

[6, 5, 3, 1, 8, 7, 2, 4]
[5, 3, 1, 2, 4]
[3, 1, 2, 4]
[1, 2]
[]
[2]
[4]
[]
[8, 7]
[7]
[]
[1, 2, 3, 4, 5, 6, 7, 8]

Despite of its simplicity, above quick sort code is not that 'quick': recursive calls keep creating new arrays which results in high space complexity. So list comprehension is not proper for quick sort implementation.

Complexity

Take a quantized look at how much space it actually cost.

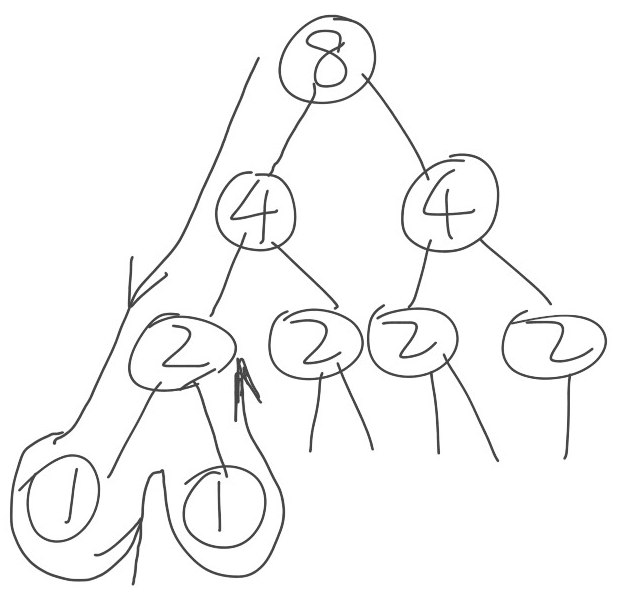
In the best case, the pivot happens to be the median value, and quick sort partition divides the sequence almost equally, so the recursions' depth is $\log n$ . As to the space complexity of each level (depth), it is worth some discussion.

A common mistake can be: each level contains $n$ elements, then the space complexity is surely $O(n)$ . The answer is right, while the approach is not. As we know, space complexity is usually measured by memory consumption of a running program. Take above out-in-place implementation as example, in the best case, each level costs half as much memory as its upper level does . Sums up to be:

$\sum _{i=0} ^{} \frac {n}{2^i} = 2n$ .

For more detail, refer to the picture below as well as above python code. The first level of recursion saves 8 values, the second 4, and so on so forth.

In the worst case, it will take $i - 1$ times of swap on level $i$ . Sums up to be:

$\sum_{i=0}^n (n-i+1) = O(n^2)$

in-place implementation

one index for partition

One in-place implementation of quick sort is to use one index for partition, as the following image illustrates. Take example of [6, 5, 3, 1, 8, 7, 2, 4] again, $l$ and $u$ stand for the lower bound and upper bound of index respectively. $i$ traverses and $m$ maintains index of partition which varies with $i$ . $target$ is the pivot.

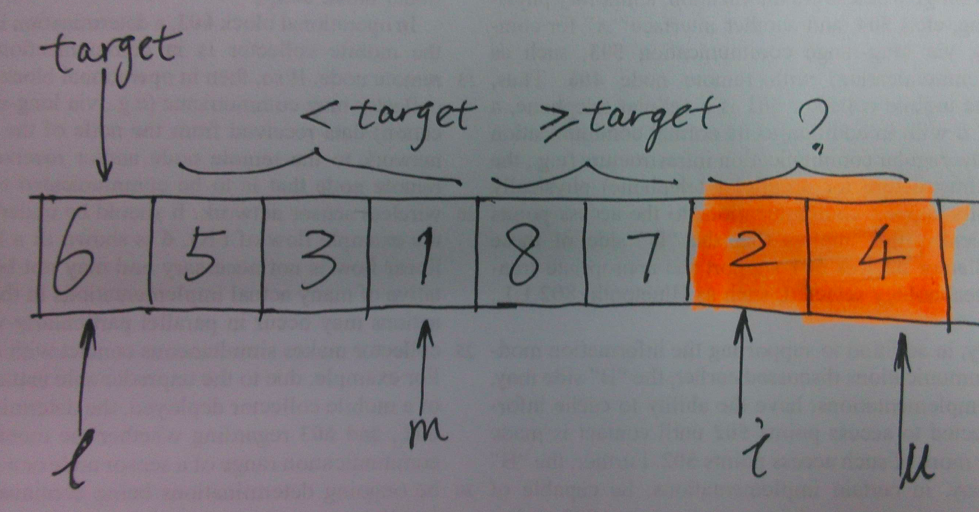
For each specific value of $i$ , $x[i]$ will take one of the follwing cases: if $x[i] \geq t$ , $i$ increases and goes on traversing; else if $x[i] < t$ , $x[i]$ will be swapped to the left part, as statement swap(x[++m], x[i]) does. Partition is done when i == u, and then we apply quick sort to the left and right parts, recursively. Under what circumstance does recursion terminate? Yes, l >= u.

Python

#!/usr/bin/env python


def qsort2(alist, l, u):
    print(alist)
    if l >= u:
        return

    m = l
    for i in xrange(l + 1, u + 1):
        if alist[i] < alist[l]:
            m += 1
            alist[m], alist[i] = alist[i], alist[m]
    # swap between m and l after partition, important!
    alist[m], alist[l] = alist[l], alist[m]
    qsort2(alist, l, m - 1)
    qsort2(alist, m + 1, u)

unsortedArray = [6, 5, 3, 1, 8, 7, 2, 4]
print(qsort2(unsortedArray, 0, len(unsortedArray) - 1))

Java

public class Sort {
    public static void main(String[] args) {
        int unsortedArray[] = new int[]{6, 5, 3, 1, 8, 7, 2, 4};
        quickSort(unsortedArray);
        System.out.println("After sort: ");
        for (int item : unsortedArray) {
            System.out.print(item + " ");
        }
    }

    public static void quickSort1(int[] array, int l, int u) {
        for (int item : array) {
            System.out.print(item + " ");
        }
        System.out.println();

        if (l >= u) return;
        int m = l;
        for (int i = l + 1; i <= u; i++) {
            if (array[i] < array[l]) {
                m += 1;
                int temp = array[m];
                array[m] = array[i];
                array[i] = temp;
            }
        }
        // swap between array[m] and array[l]
        // put pivot in the mid
        int temp = array[m];
        array[m] = array[l];
        array[l] = temp;

        quickSort1(array, l, m - 1);
        quickSort1(array, m + 1, u);
    }

    public static void quickSort(int[] array) {
        quickSort1(array, 0, array.length - 1);
    }
}

The swap of $x[i]$ and $x[m]$ should not be left out.

The output:

[6, 5, 3, 1, 8, 7, 2, 4]
[4, 5, 3, 1, 2, 6, 8, 7]
[2, 3, 1, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]

Two-way partitioning

Another implementation is to use two indexes for partition. It speeds up the partition by working two-way simultaneously, both from lower bound toward right and from upper bound toward left, instead of traversing one-way through the sequence.

The gif below shows the complete process on [6, 5, 3, 1, 8, 7, 2, 4].

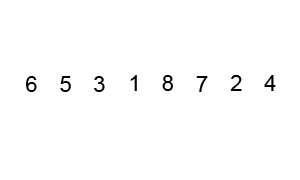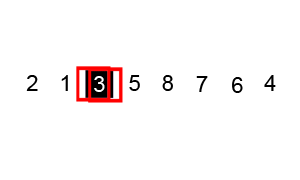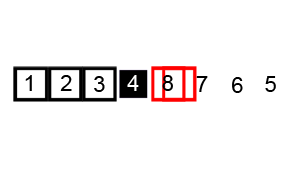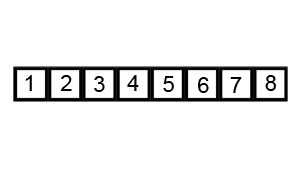
Take 3 as the pivot.
Let pointer lo start with number 6 and pointer hi start with number 4. Keep increasing lo until it comes to an element ≥ the pivot, and decreasing hi until it comes to an element < the pivot. Then swap these two elements.
Increase lo and decrease hi (both by 1), and repeat step 2 so that lo comes to 5 and hi comes to 1. Swap again.
Increase lo and decrease hi (both by 1) until they meet (at 3). The partition for pivot 3 ends. Apply the same operations on the left and right part of pivot 3.

A more general interpretation:

Init $i$ and $j$ to be at the two ends of given array.
Take the first element as the pivot.
Perform partition, which is a loop with two inner-loops:
- One that increases $i$ , until it comes to an element ≥ pivot.
- The other that decreases $j$ , until it comes to an element < pivot.
Check whether $i$ and $j$ meet or overlap. If so, swap the elements.

Think of a sequence whose elements are all equal. In such case, each partition will return the middle element, thus recursion will happen $\log n$ times. For each level of recursion, it takes $n$ times of comparison. The total comparison is $n \log n$ then. ^{programming_pearls}

Python

#!/usr/bin/env python

def qsort3(alist, lower, upper):
    print(alist)
    if lower >= upper:
        return

    pivot = alist[lower]
    left, right = lower + 1, upper
    while left <= right:
        while left <= right and alist[left] < pivot:
            left += 1
        while left <= right and alist[right] >= pivot:
            right -= 1
        if left > right:
            break
        # swap while left <= right
        alist[left], alist[right] = alist[right], alist[left]
    # swap the smaller with pivot
    alist[lower], alist[right] = alist[right], alist[lower]

    qsort3(alist, lower, right - 1)
    qsort3(alist, right + 1, upper)

unsortedArray = [6, 5, 3, 1, 8, 7, 2, 4]
print(qsort3(unsortedArray, 0, len(unsortedArray) - 1))

Java

public class Sort {
    public static void main(String[] args) {
        int unsortedArray[] = new int[]{6, 5, 3, 1, 8, 7, 2, 4};
        quickSort(unsortedArray);
        System.out.println("After sort: ");
        for (int item : unsortedArray) {
            System.out.print(item + " ");
        }
    }

    public static void quickSort2(int[] array, int l, int u) {
        for (int item : array) {
            System.out.print(item + " ");
        }
        System.out.println();

        if (l >= u) return;
        int pivot = array[l];
        int left = l + 1;
        int right = u;
        while (left <= right) {
            while (left <= right && array[left] < pivot) {
                left++;
            }
            while (left <= right && array[right] >= pivot) {
                right--;
            }
            if (left > right) break;
            // swap array[left] with array[right] while left <= right
            int temp = array[left];
            array[left] = array[right];
            array[right] = temp;
        }
        /* swap the smaller with pivot */
        int temp = array[right];
        array[right] = array[l];
        array[l] = temp;

        quickSort2(array, l, right - 1);
        quickSort2(array, right + 1, u);
    }

    public static void quickSort(int[] array) {
        quickSort2(array, 0, array.length - 1);
    }
}

The output:

[6, 5, 3, 1, 8, 7, 2, 4]
[2, 5, 3, 1, 4, 6, 7, 8]
[1, 2, 3, 5, 4, 6, 7, 8]
[1, 2, 3, 5, 4, 6, 7, 8]
[1, 2, 3, 5, 4, 6, 7, 8]
[1, 2, 3, 5, 4, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]

Having analyzed three implementations of quick sort, we may grasp one key difference between quick sort and merge sort :

Merge sort divides the original array into two sub-arrays, and merges the sorted sub-arrays to form a totally ordered one. In this case, recursion happens before processing(merging) the whole array.
Quick sort divides the original array into two sub-arrays, and then sort them. The whole array is ordered as soon as the sub-arrays get sorted. In this case, recursion happens after processing(partition) the whole array.

Robert Sedgewick's presentation on quick sort is strongly recommended.

Reference

Quicksort - wikepedia
Quicksort | Robert Sedgewick
Programming Pearls Column 11 Sorting - gives an in-depth discussion on insertion sort and quick sort
Quicksort Analysis
^{programming_pearls}. Programming Pearls ↩

Quick Sort

Quick Sort

out-in-place implementation

Complexity

in-place implementation

one index for partition

Python

Java

Two-way partitioning

Python

Java

Reference

results matching ""

No results matching ""